 Re: Pump Efficiency, Head, Flow, and related technical info
Re: Pump Efficiency, Head, Flow, and related technical info

Originally Posted by
chem geek

Just FYI. I verified that the pump in the IntelliFlo and the IntelliFlo 4x160 are identical with identical curves and efficiencies. The only difference in the full version is the addition of a flow meter plus associated electronics to keep track of total volume so that the pump can shut off after a designated number of turnovers. That is what leads to much greater savings for certain configurations where multiple features are present (needing different flow rates) or where the system curve changes (e.g. filter gets dirty).
Richard
Actually, the actual pump itself is identical with the WhisperFlo. The only difference is the motor with all it's bells and whistles.
Retired pool store and commercial pool maintenance guy.



 Reply With Quote
Reply With Quote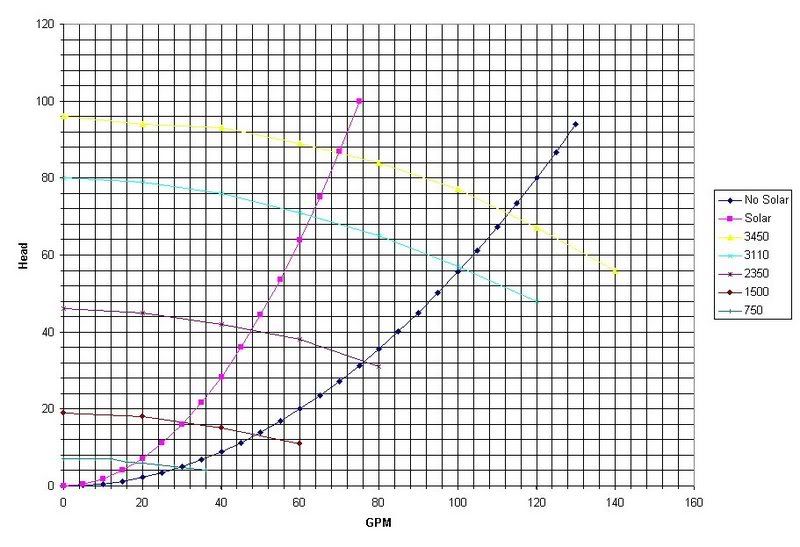




Bookmarks