Pump Efficiency, Head, Flow, and related technical info

[chem geek]

I'm adding this thread in The China Shop to move the more technical discussion that was originally started in this thread at post #14 and should get moved into this thread so that we can continue the discussion without scaring off newbies. Any net results or simple rules can be posted back into the original thread, but here in this thread we are free to use the mathematics of fluid dynamics and statics.

[chem geek]

Mark,

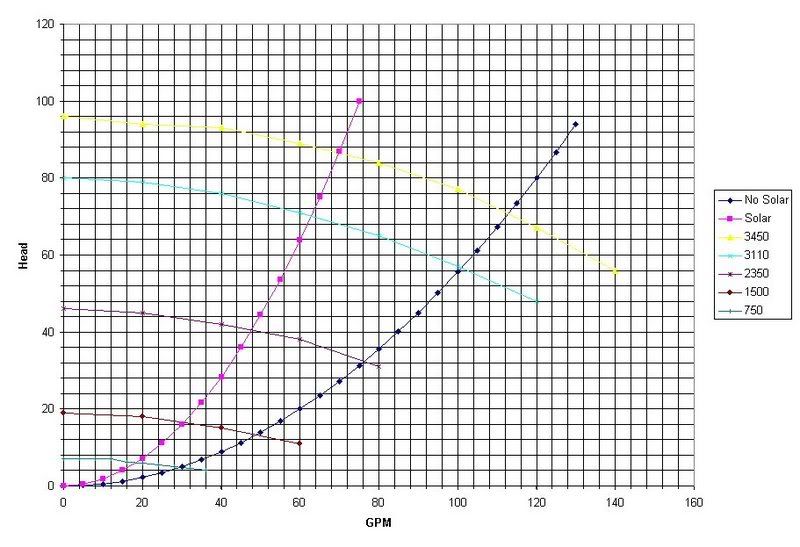
I also made a spreadsheet which is how I came up with the formula, and I carefully measured the graphs with a ruler to get reasonable accurate numbers. My data, from both the full IntelliFlow and the IntelliFlow 4x160 graphs, is as follows:
(I'm continuing to edit this to straighten out the columns)

GPM  Head  Out. Power  In. Power  Eff.  (RPM/350)^2-(GPM^2)/470
     (ft.)                                           (RPM/322)^3+80
3450 RPM
  0   96      0          1310     0.0%  97.180164    1310.277154
 20   94    353.7502     1620    21.8%  96.32910017
 40   93    699.9738     1930    36.3%  93.77590868
 60   89   1004.8011     2210    45.5%  89.52058953
 80   84   1264.4688     2510    50.4%  83.56314272
100   77   1448.8705     2780    52.1%  75.90356826
120   67   1512.8466     2980    50.8%  66.54186613
140   56   1475.2136     3010    49.0%  55.47803634

3110 RPM
  0   80      0                         78.95591837  980.9766836
 20   79    297.3007                    78.10485454
 40   76    572.0216                    75.55166305
 60   71    801.5829                    71.2963439
 80   65    978.458                     65.33889709
100   57   1072.5405                    57.67932262
120   48   1083.8304                    48.3176205
						
2350 RPM
  0   46      0                         45.08163265  468.7191816
 20   45    169.3485                    44.23056882
 40   42    316.1172                    41.67737733
 60   38    429.0162                    37.42205818
 80   31    466.6492                    31.46461138
				
2070 RPM
  0   35      0           330     0.0%  34.97877551  345.6705539
 20   34    127.9522      450    28.4%  34.12771168
 40   32    240.8512      550    43.8%  31.57452019
 60   28    316.1172      630    50.2%  27.31920104
 80   22    331.1704      690    48.0%  21.36175423

1500 RPM
  0   19      0                         18.36734694  181.0895264
 20   18     67.7394                    17.51628311
 40   15    112.899                    14.96309162
 60   11    124.1889                    10.70777247

950 RPM  chart said 750, but was probably wrong
  0   7       0                         7.367346939  105.6804838
 20   6      22.5798                    6.516283109

690 RPM
  0   4       0           95     0.0%  3.886530612   89.83965015
 20   3      11.2899      95    11.9%  3.035466782

I do not get the same data you do in your table for actual GPM. For example, at 3450 RPM and a head of 80 feet, the graph looks like this is 90 GPM, not the 97 "Actual GPM" shown in your table. I understand the pump affinity equations that are valid in regions of equivalent efficiency. I just was curiously looking for a general solution. I believe what I said before to be true, that the formula I came up with is within 1-2 feet of head in accuracy which probably means that it is accurately reflecting what is going on -- a static head based on RPM^2 minus a dynamic head based on GPM^2. The "static head" is really a balanced dynamic head between the motor pushing water one way and it leaking at the same rate the other way. The GPM^2 term appears to just be the dynamic head of the net amount of flow through the pump so while the RPM^2 "push" amount remains constant (since we are looking at a curve at constant RPM), the "leakage" amount decreases as the head decreases so that a net GPM increases. Or another way of looking at it is that the pump RPM is pushing water at a GPM determined from (RPM/350)^2-(GPM^2)/470 = 0; GPM = sqrt(470*(RPM/350)^2) = RPM/16.1 so at 3450 this is 214 GPM. So the pump's RPM (and impeller size) cause 214 GPM to move when there is no head. Any resistance (head) results in a backward "leakage" which causes the net GPM to drop (since this backward movement meets a lot of frictional resistance), but 214 GPM is always being moved "forward" by the pump even when the net GPM is 0 (meaning that the "leakage" is also 214 GPM so no net movement is seen). At least this is my best understanding of how this works. I don't have the pump curves (for this pump) going down towards 0 head, but I have seen other pumps' curves that do appear to have the parabolic shape (see this link, for example).

Regardless of which formula is used, I also wanted to estimate the electrical efficiency and that has been harder to determine. Unfortunately, only 3 RPMs showed electrical power curves on the graph so my best-guess formula isn't validated very well, but it does appear to roughly be a combination of some small fixed losses (resistance, probably) plus an amount of "work" that is related to the cube of the RPM. This makes sense since the velocity of water is proportional to the RPM as is the GPM (as shown with the formula in the previous paragraph) while the frictional losses (i.e. head) are roughly proportional to the GPM^2 so the power is expected to be the product of the flow rate times head so proportional to GPM^3 and since GPM and RPM are directly related, this is proportional to RPM^3. What is harder to figure out is how the electrical power doesn't track the output power or the amount of head as might be expected. It instead seems to have a linear increase with net GPM and then slows down its increase as it approaches around 50% efficiency. I would presume that eventually as output power dropped at lower GPM, that the electrical power would start to drop as well. The electrical power should be directly related to the pressure resistence against the impellers (I'm assuming a constant RPM) which is a difference in pressure on one side of the impeller compared to the opposite side. So normally one would expect the electrical power to be proportional to head alone, but apparently the "leakage" causes some of the pressure on the opposite side of the impeller to be higher so that the net difference isn't the full amount of head (so there is less net pressure and therefore less "work"). As the head declines, the leakage also declines and apparently reduces the pressure on the opposite side of the head faster than the overall head drop so that there is a net electrical power increase. Near the point of optimal efficiency, these two effects act so that the amount of electrical power tracks the output power (near 50% efficiency) which essentially means that the "leakage" reduces the back pressure faster than the drop in overall head, but at a rate that is similar to the output power. I suspect that in the region at lower head and high GPM that the electrical power drops in rough proportion to the head since the "leakage" effect would be much smaller at that point. So, at very low head, the pump curve should be near vertical instead of the parabolic formula that I came up with (assuming that the leakage becomes minimal at low head). It seems like I'm missing something here, at least for figuring electrical power -- either that or it truly is as complicated as it sounds and not easily computed.

Richard

[mas985]

It was probably a good idea to move this thread into the china shop. It was starting to get a bit heavy for the construction forum. Not too many people want to get into the details of hydraulics so I usually give simple approximate answers. But I tend to get a better understanding of rules of thumb by getting into the details. On to the discussion at hand………


Curve Fitting

Taking data off of a picture is bound to generate significant errors depending on who does it and how. However, I went back and looked at the chart again, I enlarged the head graph, placed grids over it and I got closer to 95 GPM so I think we are both reading it differently. Anyway, I have found that printed graphs tend to be somewhat inaccurate as well as difficult to read and I bet if you got the data directly from Pentair in tabular form, you might find it different than what is on the graph.

Static Head

Next, I wanted to more clearly define static head so there is no confusion. The classical definition of static head loss in hydraulics is vertical lift or how far the pump must lift the water in a pipe to a different elevation. This type of head loss is independent of flow rate, depends only on vertical distance traveled and is not related to pumps at all. Dynamic head loss is the opposite where it depends on the velocity of water and the pipe/fitting it is going through.

Also, the pump itself will not have any signicant amount static head loss so to describe the head equation as having a static part and a dynamic part is probably not valid. As far as the pump head curve is concerned, a pump does not care if it is subjected to static or dynamic head, head loss is head loss which is resistance to flow. However, a pump responds to different head loss with varying flow rates which is were the head curve comes from. The way I like to think of it is that the pump causes flow, the flow causes head loss in the plumbing, the head loss causes the flow to slow down in the pump and so on. It is circular but can be solved in closed form or by iteration depending on the head loss curve formula.

Pump Conservation of Energy

As for pumping theory, total energy within the pump system must be conserved where water flow is only one part of the total energy. So even if GPM decreases, it does not mean the total energy does or that it is somehow lost to “leakage”. The motor delivers energy to the shaft as BHP and the impeller then transfers that energy as both pressure and flow. So full energy transfer equations of a pump are:

Motor Formula:
Kwatts (Energy Usage) / .746 = IHP (Input Horsepower)
IHP * Motor Efficiency = BHP (Braking Horsepower)

Pump Formula (exclusive of motor)
BHP * Pumping Efficiency = WHP (Water Horsepower)

Water Horse Power Conversion Formula
WHP * 3960 = Head * GPM

So the total efficiency of a pump is
Total Pump Efficiency = Motor Efficiency * Pumping Efficiency

So as head increases and GPM decrease, WHP would be constant if the pumping efficiency stayed constant. This is the reason I started with this equation to model the head curve. However, pumping efficiency is not constant and is dependent on both flow and head, and it usually peaks near the mid point of the head curve. So GPM is not really “lost” at high head due to "leakage" but it's energy is transfered to pressure or high head such that energy is conserved via Head * GPM. So another way to think about it is those "extra" GPMs are staying in the pump housing and creating more pressure rather than leaving the pump to create flow.

Motor efficiency losses are due to the I^2R losses in the windings, electromagnetic radiation, and friction in the motor. Pumping efficiency losses are due to the friction losses in the pump housing and head losses near the impeller and before exiting the pump housing.

As you have found, motor efficiency is much more difficult to model than pumping efficiency. Few manufactures, if any, will show energy consumption as a function of motor load. As a general rule of thumb, there is a sweet spot for pumps where the pumping efficiency reaches a maximum for a particular head value and the motor efficiency also reaches a maximum for a particular head value which is usually between (75% -100% of load). Too little or too much load and the motor efficiency goes down. A well designed pump will optimize both and together they will give an optimum efficiency over a range of head values.

Just getting data on electric motor energy efficiency is difficult at best. It is usually not published or only noted as peak efficiency. A call to the manufacture may get you the data but I have not been successful to date.

Although it is a noble effort to try and model the pump with great precision, given the uncertainties involved and lack of data, I think a rough approximation of energy savings should be sufficient for economic business case to see if it is worth it. With variable speed pumps, you will get your best energy efficiency at the lowest RPM. However, you need sufficient flow to give you at most two turnovers a day which is only 22 GPM over 24 hours. Using the .03 * RPM formula gives close to 750 RPM for 22 GPM.

I am not sure what electric power curves you are referring to but if you have one for 750 RPM, then you can determine the energy usage in 24 hours and compare it to two turnovers of your existing pump and see the difference. From the data you gave previously, your old pump required 6 hours for 2 turnovers (solar off) @ 950 watts which would be 5.7 kwatts/day.

Here are a few more good papers/sites that I have found which goes over many of the details of pump and plumbing systems.

http://www.pumped101.com/efficiency.pdf
http://www.pacificliquid.com/pumpintro.pdf

[chem geek]

Mark,

I know I'm being a mensch about this, but are you looking at this PDF file on page 47 with the graph "IntelliFlo Flow and Power vs Flow Pump Curve" and then starting with 80 feet on the left and moving across that horizontal line until it intersects the black line "Head @ 3450 RPM"? It not only visually looks almost exactly halfway between the 80 and 100 vertical lines for GPM, but it measures that way also -- possibly at 91. I zoomed in a whole lot just to make sure. If I look at this PDF file which is in the 4x160 manual on page 25, then I can get something more like 92 which is getting closer to your number. Note that there are 4 vertical lines between 80 and 100 so that is 5 sections so each vertical line represents 20/5 = 4 GPM and the intersection is at the 3rd vertical line (after the 80 vertical line) so that is 12 GPM more than 80 or 92 GPM. I suspect that you counted each vertical line as being 5 GPM instead of 4. I discovered this unusual vertical line spacing (i.e. 4 lines instead of 3) because I used a ruler to measure between the two marked vertical lines (80 and 100) and didn't worry about those intermediate lines.

If you look at the first of the two links above showing the full IntelliFlo manual, then that graph does show the power (electrical) consumption curves for three RPM settings. That's how I got that data for my table.

So I looked at the documents you linked to and they are absolutely fantastic. Thank you so very much! When I referred to "leakage" it's really just a recirculation that is occurring (at a net 0 GPM and maximum head). There is no output work being done. I now see that this isn't a chamber or piston kind of pump effect, but a centrifugal impeller and vane technique so if the centrifugal added velocity goes against a pressure that brings the velocity back to zero, then there will be no net flow (but because this isn't the BEP point, there will be recirculation flows and uneven pressures in between the vanes and this can damage the pump).

The first document link you gave contained a very useful formula that helps figure out equivalent power efficiencies and identification of the most efficient point at each RPM. That is the definition of specific speed:

Ns = n * sqrt(Q) / H^(3/4)
or Specific Speed = RPM * sqrt(GPM) / (Head in Feet)^(3/4)

If I add this as a column to my spreadsheet, I find that though the specific speed varies with GPM and Head, the peak (electrical input to pump output) efficiency point at each RPM corresponds to roughly the same specific speed of around 1320. So that gives me additional useful information so that I will know if I am operating near the BEP point with both solar on and off (when I get my IntelliFlo pump).

I've made a detailed piping diagram for my system and the reason that my solar system has such high resistance is that it isn't on a single flat roof, but is on a roof with several hips so that the piping has a lot of 90 degree elbows and extra distance -- it's not at all a straight shot. There are 2 panels on one hip, 7 on another (5 higher and above 2 that are lower), 2 on another, and 1 on another. I did find a possible problem with the piping of the solar that could cause uneven flows (they didn't make the total path lengths the same throughout and instead did some Ts to return too soon so I essentially have two sets of solar panels with different path lengths). So my last 3 panels probably have lower flow than all the rest -- now I can understand why I actually saw a decrease instead of the expected increase in heat output when they added the most recent panel. They only worsened the already unbalanced situation. I'll calculate the expected flow rate difference and if it's significant, then I'll have them fix that as it should have been done correctly initially. Should be easy to fix by just breaking at the T and adding extra pipe.

Richard

[mas985]

I was using the brochure data but the manual is much better data and yes I get 92 GPM from that as well.

I can only find the energy usage curves for the Intelliflow. Are you assuming they are the same for the 4x160? I would check with Pentair on that to make sure they are the same.

Ok so with updated information, I plotted your plumbing curves (solar off/on) on top of the pump's head curve. Where they cross are your operatng points. I assumed your pump was at the same elevation as your pool.



You would get the same answer if you simultaneously solve your pump equation and your plumbing equation. So the crossover points follow the relationship of GPM = .0325 * RPM for solar off which is pretty close to what I had before. For solar on, the crossovers occur at GPM= .02 * RPM.

The only way to change your operating points is to change your plumbing. Otherwise the efficiency is what it is at those points. However, it does sound like you have an issue with your solar so if you are able to fix that it should move that curve to the right increasing the overall efficiency with solar on.

Good luck.

[mas985]

One more point that I think you touched on in your last post but I wanted to make sure it was not lost.

As you pointed out, energy use drops off as a cube of RPM so I think you will find that you will use the least amount of energy per GPM at the lowest RPM even if the efficiency drops somewhat with RPM. Assuming the maximum energy use is 3200 watts, here is my reasoning.

Watts / GPM = 3200 * (RPM/3450)^3 / GPM = 3200 * (RPM/3450)^3 / (.033 *RPM)

Watts / GPM = RPM^2 /405322.5

So the efficiency is not likely to roll off at a rate of RPM^2, so the lower the RPM the less energy is used.

Like I said before, if you operate at 750 RPM, you can do 2 turnovers in 24 hours and use the least amount of energy possible.